Emotions Struct Reference

Model that allows agents to add and parse emotions. More...

Inheritance diagram for Emotions:

Collaboration diagram for Emotions:

Public Member Functions
	Emotions (Construct &construct)
	Checks for the agent node attributes "can send emotion" and "can receive emotion" and adds the emotion nodeset's names to InteractionItem::item_names.
virtual std::map< unsigned int, float >	get_emotions (unsigned int agent_index)
	Determines which emotions to attach to a message. More...
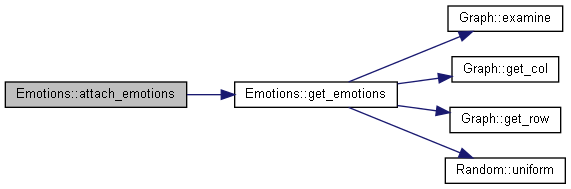
virtual void	attach_emotions (unsigned int sender_index, InteractionItem *item)
	Takes the output from Emotions::get_emotions ands the corresponding elements to an InteractionItem. More...
virtual std::map< unsigned int, float >	parse_emotions (const InteractionItem &values)
	Parses an InteractionItem and converts it to a map that contains only values corresponding to an emotion node. More...
virtual void	read_emotions (const std::map< unsigned int, float > &attached_emotions, unsigned int agent_index)
	Updates the agent's emotions based on the attached emotions. More...
void	update_item_names (void)
	Adds the names of emotion nodes to InteractionItem::item_names. More...
bool	intercept (InteractionItem &item, unsigned int sender, unsigned int receiver, const CommunicationMedium *medium) override
	Each message in the queue has some, none, or all emotions attached to it. More...
void	communicate (const InteractionMessage &msg) override
	Each message is parsed for attached emotions which update the receiver's emotional state. More...
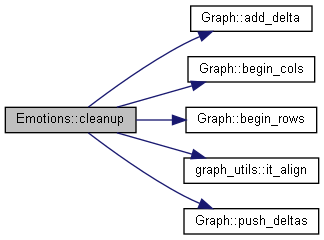
void	cleanup (void) override
	Each agent self-regulates their emotions to return to their base emotional state. More...
Public Member Functions inherited from Model
	Model (Construct &_construct)
	Constructor for all models in Construct. More...
virtual	~Model (void)
	Virtual Deconstructor. More...
virtual void	initialize (void)
	Function called once before any simulation cycles begin. More...
virtual void	think (void)
	First function called in a simulation cycle. More...
virtual void	update (void)
	Function called after the think functions in a simulation cycle. More...
virtual bool	intercept (InteractionItem &item, unsigned int sender, unsigned int receiver, const CommunicationMedium *medium)
	Allows for models to effect change to items created by other models. More...
virtual void	communicate (const InteractionMessage &msg)
	Function called after the update functions in a simulation cycle. More...
virtual void	cleanup (void)
	Function called after the Model::communicate functions in a simulation cycle. More...
void	add_base_model_to_model_manager (const std::string &base_model_name)
	Adds a derived model under the name of the base model and disables the model manager from calling its functions.

Public Attributes
const Nodeset &	agents = ns_manager.get_nodeset(nodeset_names::agents)
const Nodeset &	emotions = ns_manager.get_nodeset(nodeset_names::emotions)
Graph< float > &	emotion_net = graph_manager.load_required(graph_names::emotion_net, agents, emotions)
	Each link holds the emotional value of each agent for each emotion. More...
const Graph< float > &	emot_broadcast_bias = graph_manager.load_optional(graph_names::emot_broad_bias, 1.0f, agents, false, emotions, false)
	The base probability an agent attaches an emotion. More...
const Graph< float > &	emot_broadcast_first = graph_manager.load_optional(graph_names::emot_broad_first, 0.0f, emotions, false, emotions, false)
	The first order emotional dependence on the probability an agent attaches an emotion. More...
const Graph< std::map< unsigned int, float > > &	emot_broadcast_second
	The second order emotional dependence on the probability an agent attaches an emotion. More...
const Graph< float > &	emot_reading_first = graph_manager.load_required(graph_names::emot_read_first, emotions, emotions)
	The first order emotional dependence on the deflection from reading an emotional message. More...
const Graph< std::map< unsigned int, float > > &	emot_reading_second
	The second order emotional dependence on the deflection from reading an emotional message. More...
const Graph< float > &	emot_regulation_bias = graph_manager.load_required(graph_names::emot_reg_bias, agents, emotions)
	The base emotion-independent dependence on the self-regulation of emotion. More...
const Graph< float > &	emot_regulation_first = graph_manager.load_required(graph_names::emot_reg_first, emotions, emotions)
	The first order emotional dependence on the self-regulation of emotion. More...
const Graph< std::map< unsigned int, float > > &	emot_regulation_second
	The second order emotional dependence on the self-regulation of emotion. More...
Public Attributes inherited from Model
Construct &	construct
GraphManager &	graph_manager
NodesetManager &	ns_manager
Random &	random
bool	valid
	If member is false, the model's functions are not called.

Static Public Attributes
static constexpr char	emot_itemkey_block = 100
	Defines the start of the reserved block of keys for emotions in InteractionItem::item_keys More...

Detailed Description

Model that allows agents to add and parse emotions.

Agents may attach the emotions of the sender of a messages during the update function. Emotions are added probabilistically based on the agent's current emotional state. Agents then parse the emotions of those that they receive messages from. Emotions of the ego agent is updated based on their current emotional state and the emotions contained in the message. Finally, agents self-regulate their emotions during the clean_up step to either increase or decrease their emotional value.

Member Function Documentation

attach_emotions()

void Emotions::attach_emotions ( unsigned int  sender_index, InteractionItem *  item  )

virtual

Takes the output from Emotions::get_emotions ands the corresponding elements to an InteractionItem.

For each element in the output from Emotions::get_emotions, the key is converted to an InteractionItem::item_keys after adding Emotions::emot_itemkey_block to it and then stored in InteractionItem::values. InteractionItem::item_keys::emotion is then added to InteractionItem::attributes.

Here is the call graph for this function:

Here is the caller graph for this function:

cleanup()

void Emotions::cleanup ( void  )

overridevirtual

Each agent self-regulates their emotions to return to their base emotional state.

Each agent \(i\) updates their emotion \(n\) by \(E^'_{i,n}=A_{i,n}+\sum_mB_{n,m}E_{i,m}+\sum_{m,g}C_{n,m,g}E_{i,m}E_{i,g}\), where \(A\) is the "emotion regulation bias network", \(B\) is the "first order emotion regulation network", \(C\) is the "second order emotion regulation network", \(E\) is the "emotion network", and \(E^'\) is the updates to the emotion network.

Reimplemented from Model.

Here is the call graph for this function:

communicate()

void Emotions::communicate ( const InteractionMessage &  msg )

overridevirtual

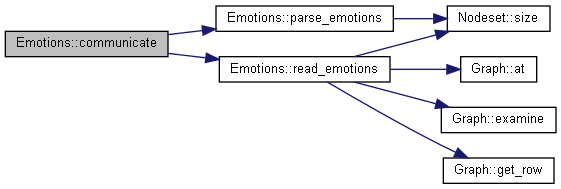
Each message is parsed for attached emotions which update the receiver's emotional state.

The message is scanned for all emotion items. For each of these items, its emotion index and emotional value pair is added to a map that is eventually passed to read_emotions to update the receiver's emotional state.

Reimplemented from Model.

Here is the call graph for this function:

get_emotions()

std::map< unsigned int, float > Emotions::get_emotions ( unsigned int  agent_index )

virtual

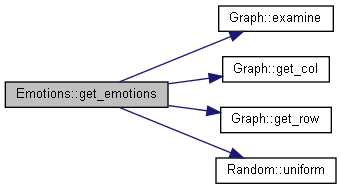
Determines which emotions to attach to a message.

The equation for calcuating the probability the agent_index \(i\) will attach emotion \(n\) is \(P^{(attach)}_{i,n}=A_{i,n}+\sum_mB_{n,m}E_{i,m}+\sum_{m,g}C_{n,m,g}E_{i,m}E_{i,g}\) where \(A\) is the "emotion broadcast bias network", \(B\) is the "first order emotion broadcast network", \(C\) is the "second order emotion broadcast network", and \(E\) is the "emotion network".

Returns

A map whose pair elements correspond to emotional indexes and their respective emotional value.

Here is the call graph for this function:

Here is the caller graph for this function:

intercept()

bool Emotions::intercept ( InteractionItem &  item, unsigned int  sender, unsigned int  receiver, const CommunicationMedium *  medium  )

overridevirtual

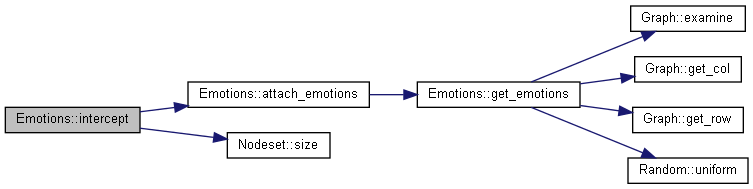
Each message in the queue has some, none, or all emotions attached to it.

Using the result from get_emotions, each attached emotion is added to the message as its own InteractionItem. Emotion items use the InteractionItem::item_keys::emotion key. This key is added to InteractionItem::attributes. The emotion index is stored using this key in InteractionItem::indexes and the emotional value is stored using this key in InteracionItem::values.

Reimplemented from Model.

Here is the call graph for this function:

parse_emotions()

std::map< unsigned int, float > Emotions::parse_emotions ( const InteractionItem &  values )

virtual

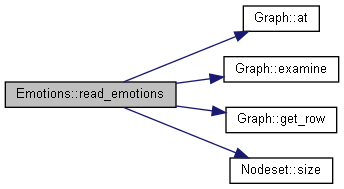
Parses an InteractionItem and converts it to a map that contains only values corresponding to an emotion node.

If the item doesn't contain InteractionItem::item_keys::emotion in its attributes, an empty map is returned. Otherwise, for each element in InteractionItem::values, if the key when converted to a char is greater than Emotions::emot_itemkey_block, That value is added to the returned map with a key equal to item's key minus Emotions::emot_itemkey_block. An assertion is raised if the item's key is larger than or equal to Emotions::emot_itemkey_block + the emotion nodeset's size.

Returns

A map whose pair elements correspond to emotional indexes and their respective emotional value.

Here is the call graph for this function:

Here is the caller graph for this function:

read_emotions()

void Emotions::read_emotions ( const std::map< unsigned int, float > &  attached_emotions, unsigned int  agent_index  )

virtual

Updates the agent's emotions based on the attached emotions.

The equation for calcuating the updated emotional value for emotion \(n\)m for the agent_index \(i\) with \(\tau\) being the attached emotions is \(E^{'}_{i,n}=\frac{1}{1+exp\left[ -\sum_mB_{n,m}\tau_m-\sum_{m,g}C_{n,m,g}\tau_m\tau_g +ln\left( 1-\frac{1}{E_{i,n}}\right)\right]}\) where \(B\) is the "first order emotion reading network", \(C\) is the "second order emotion reading network", and \(E\) is the "emotion network".

Here is the call graph for this function:

Here is the caller graph for this function:

update_item_names()

void Emotions::update_item_names ( void  )

inline

Adds the names of emotion nodes to InteractionItem::item_names.

The names are added at a key equal to the node's index plus Emotions::emot_itemkey_block. Assertion can be raised if a name already exists at a key reserved by the block.

Here is the caller graph for this function:

Member Data Documentation

agents

const Nodeset& Emotions::agents = ns_manager.get_nodeset(nodeset_names::agents)

summary>

emot_broadcast_bias

const Graph<float>& Emotions::emot_broadcast_bias = graph_manager.load_optional(graph_names::emot_broad_bias, 1.0f, agents, false, emotions, false)

The base probability an agent attaches an emotion.

Dimensions: agent x emotion
This network is a part of the equation for calculating the probability that an agent attaches an emotion to a message they send. The probability agent \(i\) attaches emotion \(n\) is \(P_{i,n}=A_{i,n}+\sum_mB_{n,m}E_{i,m}+\sum_{m,g}C_{n,m,g}E_{i,m}E_{i,g}\) where \(A_{i,n}\) corresponds to links in this network.

emot_broadcast_first

const Graph<float>& Emotions::emot_broadcast_first = graph_manager.load_optional(graph_names::emot_broad_first, 0.0f, emotions, false, emotions, false)

The first order emotional dependence on the probability an agent attaches an emotion.

Dimensions: emotion x emotion
This network is a part of the equation for calculating the probability that an agent attaches an emotion to a message they send. The probability agent \(i\) attaches emotion \(n\) is \(P_{i,n}=A_{i,n}+\sum_mB_{n,m}E_{i,m}+\sum_{m,g}C_{n,m,g}E_{i,m}E_{i,g}\) where \(B_{n,m}\) corresponds to links in this network and \(E_{i,m}\) is the agent's emotional value for emotion \(m\).

emot_broadcast_second

const Graph<std::map<unsigned int, float> >& Emotions::emot_broadcast_second

Initial value:

= 
        graph_manager.load_optional(graph_names::emot_broad_second, std::map<unsigned int, float>(), emotions, false, emotions, false, emotions)

The second order emotional dependence on the probability an agent attaches an emotion.

Dimensions: emotion x emotion x emotion
This network is a part of the equation for calculating the probability that an agent attaches an emotion to a message they send. The probability agent \(i\) attaches emotion \(n\) is \(P_{i,n}=A_{i,n}+\sum_mB_{n,m}E_{i,m}+\sum_{m,g}C_{n,m,g}E_{i,m}E_{i,g}\) where \(C_{n,m,g}\) corresponds to links in this network and \(E_{i,m}\) is the agent's emotional value for emotion \(m\).

emot_itemkey_block

constexpr char Emotions::emot_itemkey_block = 100

staticconstexpr

Defines the start of the reserved block of keys for emotions in InteractionItem::item_keys

When referencing an emotion in an InteractionItem, the node's index is equal to the key in the item minus this member.

summary>

emot_reading_first

const Graph<float>& Emotions::emot_reading_first = graph_manager.load_required(graph_names::emot_read_first, emotions, emotions)

The first order emotional dependence on the deflection from reading an emotional message.

Dimensions: emotion x emotion
This network is a part of the equation for calculating the deflection of an emotion in response to reading an emotional message. Positive deflection increases the emotional value, negative decreases, and a deflection of zero does not change the emotional value. The deflection of emotion \(n\) for agent \(i\) is \(D_{i,n}=\sum_mB_{n,m}\tau_{m}+\sum_{m,g}C_{n,m,g}\tau_m\tau_g\) where \(B_{n,m}\) are links in this network and \(\tau_m\) is the emotional value contained in the read message for emotion \(m\).

emot_reading_second

const Graph<std::map<unsigned int, float> >& Emotions::emot_reading_second

Initial value:

=
        graph_manager.load_optional(graph_names::emot_read_second, std::map<unsigned int, float>(), emotions, false, emotions, false, emotions)

The second order emotional dependence on the deflection from reading an emotional message.

Dimensions: emotion x emotion x emotion
This network is a part of the equation for calculating the deflection of an emotion in response to reading an emotional message. Positive deflection increases the emotional value, negative decreases, and a deflection of zero does not change the emotional value. The deflection of emotion \(n\) for agent \(i\) is \(D_{i,n}=\sum_mB_{n,m}\tau_{m}+\sum_{m,g}C_{n,m,g}\tau_m\tau_g\) where \(C_{n,m,g}\) are links in this network and \(\tau_m\) is the emotional value contained in the read message for emotion \(m\).

emot_regulation_bias

const Graph<float>& Emotions::emot_regulation_bias = graph_manager.load_required(graph_names::emot_reg_bias, agents, emotions)

The base emotion-independent dependence on the self-regulation of emotion.

Dimensions: agent x emotion
This network is a part of the equation for updating an agent's emotional state each time step. The updated emotional value for emotion \(n\) for agent \(i\) is \(E^{'}_{i,n}=A_{i,n}\sum_mB_{n,m}\E_{i,m}+\sum_{m,g}C_{n,m,g}E_{i,m}E_{i,g}\) where \(A_{i,n}\) are links in this network and \(E_{i,m}\) is the agent's emotional value for emotion \(m\).

emot_regulation_first

const Graph<float>& Emotions::emot_regulation_first = graph_manager.load_required(graph_names::emot_reg_first, emotions, emotions)

The first order emotional dependence on the self-regulation of emotion.

Dimensions: emotion x emotion
This network is a part of the equation for updating an agent's emotional state each time step. The updated emotional value for emotion \(n\) for agent \(i\) is \(E^{'}_{i,n}=A_{i,n}\sum_mB_{n,m}\E_{i,m}+\sum_{m,g}C_{n,m,g}E_{i,m}E_{i,g}\) where \(B_{n,m}\) are links in this network and \(E_{i,m}\) is the agent's emotional value for emotion \(m\).

emot_regulation_second

const Graph<std::map<unsigned int, float> >& Emotions::emot_regulation_second

Initial value:

=
        graph_manager.load_optional(graph_names::emot_reg_second, std::map<unsigned int, float>(), emotions, false, emotions, false, emotions)

The second order emotional dependence on the self-regulation of emotion.

Dimensions: agent x emotion
This network is a part of the equation for updating an agent's emotional state each time step. The updated emotional value for emotion \(n\) for agent \(i\) is \(E^{'}_{i,n}=A_{i,n}\sum_mB_{n,m}\E_{i,m}+\sum_{m,g}C_{n,m,g}E_{i,m}E_{i,g}\) where \(C_{n,m,g}\) are links in this network and \(E_{i,m}\) is the agent's emotional value for emotion \(m\).

emotion_net

Graph<float>& Emotions::emotion_net = graph_manager.load_required(graph_names::emotion_net, agents, emotions)

Each link holds the emotional value of each agent for each emotion.

Dimensions: agent x emotion